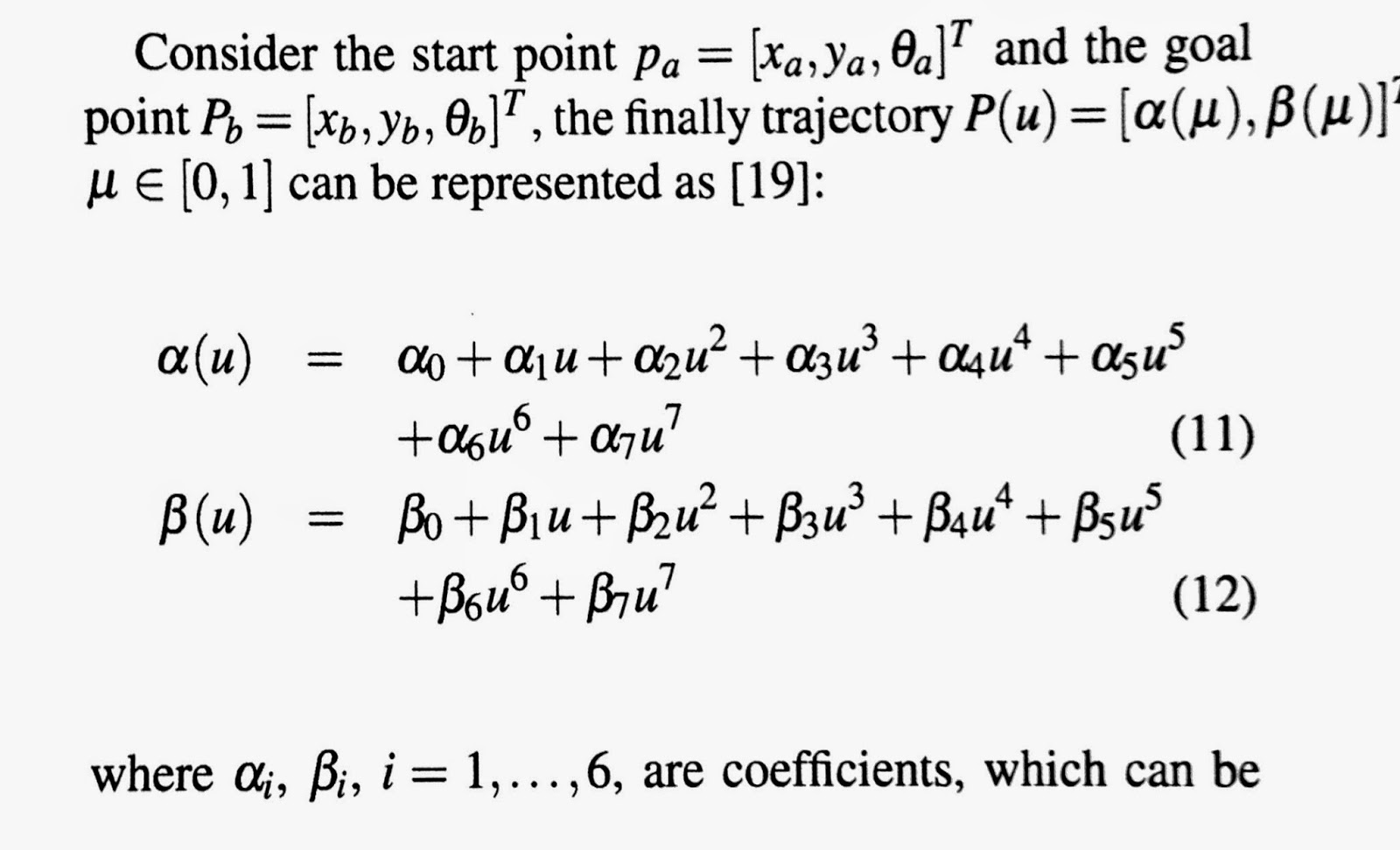지금 사용하고 있는 opencv 버전의 설치 위치인
D:\opencv 2.4.9\build\python\2.7\x86
에 있는
cv2.pyd 파일을 다음 위치로 복사한다.
C:\Python27\Lib\site-packages
Python IDLE에서
>>import cv2
특별한 함수가 설치되었는지 유무는
>>help(cv2.SIFT())
또는
>>help(cv2)
등으로 체크할 수 있다.
참고
[1] http://imky.egloos.com/2969966
2014년 12월 22일 월요일
2014년 12월 1일 월요일
OpenCV - Color image In/Out
#pragma once
#include <iostream>
#include <opencv/cv.h>
#include <opencv/highgui.h>
using namespace std;
using namespace cv;
// Write grayscale image
void WriteIm(String str, unsigned char* im, const Size& sz)
{
Mat bIm = Mat(sz.height, sz.width, CV_8UC1, im);
imwrite(str, bIm);
}
void main()
{
Mat image = imread("face.jpg");
if (image.empty()) return;
cv::Size sz = image.size();
// hsl channel split
Mat hsl;
cvtColor(image, hsl, CV_RGB2HLS);
Mat hslChannels[3];
split(hsl, hslChannels);
unsigned char *im_l = hslChannels[1].ptr<unsigned char>();
unsigned char *im_h = hslChannels[0].ptr<unsigned char>();
unsigned char *im_s = hslChannels[2].ptr<unsigned char>();
// rgb channel split
Mat rgbChannels[3];
split(image, rgbChannels);
unsigned char *im_r = rgbChannels[0].ptr<unsigned char>();
unsigned char *im_g = rgbChannels[1].ptr<unsigned char>();
unsigned char *im_b = rgbChannels[2].ptr<unsigned char>();
// access image pointer
for(int i=0; i<sz.height; i++)
{
for(int j=0; j<sz.width; j++)
{
im_r[i*sz.width+j] = 255 - im_r[i*sz.width+j];
}
}
// Write image
WriteIm("inv_red.jpg", im_r, sz);
waitKey();
}
#include <iostream>
#include <opencv/cv.h>
#include <opencv/highgui.h>
using namespace std;
using namespace cv;
// Write grayscale image
void WriteIm(String str, unsigned char* im, const Size& sz)
{
Mat bIm = Mat(sz.height, sz.width, CV_8UC1, im);
imwrite(str, bIm);
}
void main()
{
Mat image = imread("face.jpg");
if (image.empty()) return;
cv::Size sz = image.size();
// hsl channel split
Mat hsl;
cvtColor(image, hsl, CV_RGB2HLS);
Mat hslChannels[3];
split(hsl, hslChannels);
unsigned char *im_l = hslChannels[1].ptr<unsigned char>();
unsigned char *im_h = hslChannels[0].ptr<unsigned char>();
unsigned char *im_s = hslChannels[2].ptr<unsigned char>();
// rgb channel split
Mat rgbChannels[3];
split(image, rgbChannels);
unsigned char *im_r = rgbChannels[0].ptr<unsigned char>();
unsigned char *im_g = rgbChannels[1].ptr<unsigned char>();
unsigned char *im_b = rgbChannels[2].ptr<unsigned char>();
// access image pointer
for(int i=0; i<sz.height; i++)
{
for(int j=0; j<sz.width; j++)
{
im_r[i*sz.width+j] = 255 - im_r[i*sz.width+j];
}
}
// Write image
WriteIm("inv_red.jpg", im_r, sz);
waitKey();
}
2014년 11월 30일 일요일
Python에서 sqlite를 이용한 BoVW 구현
# Python에서 sqlite를 이용한 BoVW 구현
# funMV, 2014.12
from numpy import *
import pickle
from pysqlite2 import dbapi2 as sqlite
import sift
import imagesearch
f = open("ukbench/first1000/list.txt",'r') # to access sub-directory
lines = f.readlines() # read all lines through line to line style
f.close()
imlist=[ 'ukbench/first1000/'+line[:-1] for line in lines] # to eliminate last character '\n'
nbr_images=len(imlist)
featlist=[ imlist[i][:-3]+'sift' for i in range(nbr_images)] # filename.sift in each line
# load vocabulary
with open('vocabulary.pkl','rb') as f:
voc = pickle.load(f)
# create db
con = sqlite.connect('test1.db') # 재 실행시, 반드시 test1.db를 지우고 돌려야 함
# 일단, 실행되면 hdd에 test1.db가 저장되기 때문
# create tables
con.execute('create table imlist(filename)')
con.execute('create table imwords(imid,wordid,vocname)')
con.execute('create table imhistograms(imid,histogram,vocname)')
# 다음 4개 명령은 없어도 실행되지만 좀 느려지는 것 같음
con.execute('create index im_idx on imlist(filename)')
con.execute('create index wordid_idx on imwords(wordid)')
con.execute('create index imid_idx on imwords(imid)')
con.execute('create index imidhist_idx on imhistograms(imid)')
con.commit()
# test db
locs, descr = sift.read_features_from_file(featlist[0])
# locs=2276x4, descr=2276x128
# For first image, 2277 features are there and they will be prjected to vw
imwords=voc.project(descr)
#voc.shape[0]=498: # of visual words
#imwords.shape=498의 히스토그램(보팅) 정보
#imwords: voting number of features per each word (histogram). some features among 2278 features
# are voted 7 times to first word, and 6 times for second words of vw, so on.
#array([ 7., 6., 2., 1., 5., 4., 4., 1., 0., 4., 2.,
# 3., 6., 1., 2., 4., 2., 0., 1., 9., 1., 1.,
# 2., 3., 0., 1., 7., 3., 2., 7., 3., 0., 5.,
# 17., 1., 3., 16., 6., 3., 8., 26., 11., 1., 10.,
# 3., 3., 4., 2., 2., 1., 2., 1., 2., 2., ...
nbr_words=imwords.shape[0] # 498
# 위는 test모드이고 여기서부터는 실제 모든 im의 feature들을 db에 삽입
# go through all images, project features on vocabulary and insert
for i in range(nbr_images)[:100]: # [0,1,2,...,98,99]
locs, descr = sift.read_features_from_file(featlist[i])
imname = imlist[i]
imwords=voc.project(descr)
nbr_words=imwords.shape[0]
# (1) 파일 이름을 db에 저장
cur=con.execute("insert into imlist(filename) values ('%s')" %imname)
imid = cur.lastrowid
# (2) 파일 이름 id - 각 word에 대한 voting 횟수 연계 저장
for j in range(nbr_words):
word = imwords[j]
con.execute("insert into imwords(imid,wordid,vocname) values (?,?,?)",
(imid,word,voc.name))
# (3) 파일이름 id와 히스토그램 전체 저장
con.execute("insert into imhistograms(imid,histogram,vocname) values (?,?,?)",
(imid,pickle.dumps(imwords),voc.name))
# 여기서 최종 결과를 저장하고 나가려면 commit를 해 주여야 함.
# con.commit()
# 다시 사용 시
# con=sqlite.connect('test1.db')
#
# Test for saved db
print con.execute('select count (filename) from imlist').fetchone()
# (100,), 100개의 im name이 저장
print con.execute('select * from imlist').fetchone()
# (u'ukbench/first1000/ukbench00000.jpg',)
##################################################
# 여기서 부터 저장된 db를 이용한 test
##################################################
# test할 query인 첫번째 im의 id, 히스토그램을 가져옴
im_id = con.execute("select rowid from imlist where filename='%s'" % imlist[0]).fetchone()
#im_id=(1,)
s = con.execute("select histogram from imhistograms where rowid='%d'" % im_id).fetchone()
h = pickle.loads(str(s[0])) # len(.)=498, histogram for word voting
#Using the index to get candidates
#locs, descr = sift.read_features_from_file(featlist[0])
#imwords=voc.project(descr)
#words=imwords.nonzero()[0] #voting이 하나라도 있는 words의 index
words=h.nonzero()[0]
#vw에 대한 histogram(bin수는 보팅 횟수가 0인 빈을 배제 후 vw의 갯수 만큼)
# words.shape=(455,)=[0,1,2,3,5,....]
# find candidates
candidates = []
for word in words:
# table imword에서 word id로 imid를 추출. 즉, 특정 word를 가진 모든 im의 id를 추출
# 즉, query im의 해당 word를 가지는 db내 모든 im의 id 리스트를 candidates에 저장
im_ids = con.execute("select distinct imid from imwords where wordid=%d"
% word).fetchall()
c = [i[0] for i in im_ids]
candidates += c
# len(candidates) = 1443
# take all unique words and reverse sort on occurrence
tmp = [(w,candidates.count(w)) for w in set(candidates)]
# candidates.count(1)=23, candidates.count(10)=15
# set(candidates)=[1,2,3,4,...,99,100]
# tmp=[(1, 23), (2, 23), (3, 19), (4, 26), (5, 11), (6, 13), (7, 14),
# (8, 11), (9, 28), (10, 15), (11, 14), (12, 30), (13, 10),.....
# (95, 27), (96, 31), (97, 19), (98, 16), (99, 18), (100, 17)]
tmp.sort(cmp=lambda x,y:cmp(x[1],y[1]))
tmp.reverse()
candi=[w[0] for w in tmp] # len(candi)=100
#candi=[43,77,44,42,78,79,...,21,84,83]
#필요한 것은 im의 id이므로 sort후 reverse해줌
matchscores=[]
for imid in candi:
s = con.execute("select histogram from imhistograms where rowid='%d'" % imid).fetchone()
cand_h = pickle.loads(str(s[0])) # histogram for word voting
cand_dist = sqrt( sum( voc.idf*(h-cand_h)**2 ) )
matchscores.append( (cand_dist,imid) )
matchscores.sort()
print matchscores[:10]
#[(0.0, 1), (60.812088499474271, 2), (61.547483004618186, 3), (92.620967753952812, 4),
# (100.59065889285603, 34), (107.76370948763174, 28), (108.27892205906744, 25),
# (109.39719124624605, 9), (110.33866766043165, 10), (110.77231202013482, 20)]
con.commit()
con.close()
# funMV, 2014.12
from numpy import *
import pickle
from pysqlite2 import dbapi2 as sqlite
import sift
import imagesearch
f = open("ukbench/first1000/list.txt",'r') # to access sub-directory
lines = f.readlines() # read all lines through line to line style
f.close()
imlist=[ 'ukbench/first1000/'+line[:-1] for line in lines] # to eliminate last character '\n'
nbr_images=len(imlist)
featlist=[ imlist[i][:-3]+'sift' for i in range(nbr_images)] # filename.sift in each line
# load vocabulary
with open('vocabulary.pkl','rb') as f:
voc = pickle.load(f)
# create db
con = sqlite.connect('test1.db') # 재 실행시, 반드시 test1.db를 지우고 돌려야 함
# 일단, 실행되면 hdd에 test1.db가 저장되기 때문
# create tables
con.execute('create table imlist(filename)')
con.execute('create table imwords(imid,wordid,vocname)')
con.execute('create table imhistograms(imid,histogram,vocname)')
# 다음 4개 명령은 없어도 실행되지만 좀 느려지는 것 같음
con.execute('create index im_idx on imlist(filename)')
con.execute('create index wordid_idx on imwords(wordid)')
con.execute('create index imid_idx on imwords(imid)')
con.execute('create index imidhist_idx on imhistograms(imid)')
con.commit()
# test db
locs, descr = sift.read_features_from_file(featlist[0])
# locs=2276x4, descr=2276x128
# For first image, 2277 features are there and they will be prjected to vw
imwords=voc.project(descr)
#voc.shape[0]=498: # of visual words
#imwords.shape=498의 히스토그램(보팅) 정보
#imwords: voting number of features per each word (histogram). some features among 2278 features
# are voted 7 times to first word, and 6 times for second words of vw, so on.
#array([ 7., 6., 2., 1., 5., 4., 4., 1., 0., 4., 2.,
# 3., 6., 1., 2., 4., 2., 0., 1., 9., 1., 1.,
# 2., 3., 0., 1., 7., 3., 2., 7., 3., 0., 5.,
# 17., 1., 3., 16., 6., 3., 8., 26., 11., 1., 10.,
# 3., 3., 4., 2., 2., 1., 2., 1., 2., 2., ...
nbr_words=imwords.shape[0] # 498
# 위는 test모드이고 여기서부터는 실제 모든 im의 feature들을 db에 삽입
# go through all images, project features on vocabulary and insert
for i in range(nbr_images)[:100]: # [0,1,2,...,98,99]
locs, descr = sift.read_features_from_file(featlist[i])
imname = imlist[i]
imwords=voc.project(descr)
nbr_words=imwords.shape[0]
# (1) 파일 이름을 db에 저장
cur=con.execute("insert into imlist(filename) values ('%s')" %imname)
imid = cur.lastrowid
# (2) 파일 이름 id - 각 word에 대한 voting 횟수 연계 저장
for j in range(nbr_words):
word = imwords[j]
con.execute("insert into imwords(imid,wordid,vocname) values (?,?,?)",
(imid,word,voc.name))
# (3) 파일이름 id와 히스토그램 전체 저장
con.execute("insert into imhistograms(imid,histogram,vocname) values (?,?,?)",
(imid,pickle.dumps(imwords),voc.name))
# 여기서 최종 결과를 저장하고 나가려면 commit를 해 주여야 함.
# con.commit()
# 다시 사용 시
# con=sqlite.connect('test1.db')
#
# Test for saved db
print con.execute('select count (filename) from imlist').fetchone()
# (100,), 100개의 im name이 저장
print con.execute('select * from imlist').fetchone()
# (u'ukbench/first1000/ukbench00000.jpg',)
##################################################
# 여기서 부터 저장된 db를 이용한 test
##################################################
# test할 query인 첫번째 im의 id, 히스토그램을 가져옴
im_id = con.execute("select rowid from imlist where filename='%s'" % imlist[0]).fetchone()
#im_id=(1,)
s = con.execute("select histogram from imhistograms where rowid='%d'" % im_id).fetchone()
h = pickle.loads(str(s[0])) # len(.)=498, histogram for word voting
#Using the index to get candidates
#locs, descr = sift.read_features_from_file(featlist[0])
#imwords=voc.project(descr)
#words=imwords.nonzero()[0] #voting이 하나라도 있는 words의 index
words=h.nonzero()[0]
#vw에 대한 histogram(bin수는 보팅 횟수가 0인 빈을 배제 후 vw의 갯수 만큼)
# words.shape=(455,)=[0,1,2,3,5,....]
# find candidates
candidates = []
for word in words:
# table imword에서 word id로 imid를 추출. 즉, 특정 word를 가진 모든 im의 id를 추출
# 즉, query im의 해당 word를 가지는 db내 모든 im의 id 리스트를 candidates에 저장
im_ids = con.execute("select distinct imid from imwords where wordid=%d"
% word).fetchall()
c = [i[0] for i in im_ids]
candidates += c
# len(candidates) = 1443
# take all unique words and reverse sort on occurrence
tmp = [(w,candidates.count(w)) for w in set(candidates)]
# candidates.count(1)=23, candidates.count(10)=15
# set(candidates)=[1,2,3,4,...,99,100]
# tmp=[(1, 23), (2, 23), (3, 19), (4, 26), (5, 11), (6, 13), (7, 14),
# (8, 11), (9, 28), (10, 15), (11, 14), (12, 30), (13, 10),.....
# (95, 27), (96, 31), (97, 19), (98, 16), (99, 18), (100, 17)]
tmp.sort(cmp=lambda x,y:cmp(x[1],y[1]))
tmp.reverse()
candi=[w[0] for w in tmp] # len(candi)=100
#candi=[43,77,44,42,78,79,...,21,84,83]
#필요한 것은 im의 id이므로 sort후 reverse해줌
matchscores=[]
for imid in candi:
s = con.execute("select histogram from imhistograms where rowid='%d'" % imid).fetchone()
cand_h = pickle.loads(str(s[0])) # histogram for word voting
cand_dist = sqrt( sum( voc.idf*(h-cand_h)**2 ) )
matchscores.append( (cand_dist,imid) )
matchscores.sort()
print matchscores[:10]
#[(0.0, 1), (60.812088499474271, 2), (61.547483004618186, 3), (92.620967753952812, 4),
# (100.59065889285603, 34), (107.76370948763174, 28), (108.27892205906744, 25),
# (109.39719124624605, 9), (110.33866766043165, 10), (110.77231202013482, 20)]
con.commit()
con.close()
Bag of Visual Words
Bag of Words의 요약:
# BoW를 이해하기 위한 Toy example
# BoW algorithm analysis
# 2013/06/28, 2014/12/03 개선
# by funmv
#
from PIL import Image
from pylab import *
import os
from numpy import *
from scipy.cluster.vq import *
import sift
import vocabulary
# 물체의 class는 3개이다 (즉, 0~3/4~7/8~11의 4개씩 동일 물체를 다른 자세에서 찍었음. 아래 그림 참조)
imlist = ['ukbench00000.jpg', 'ukbench00001.jpg', 'ukbench00002.jpg', 'ukbench00003.jpg', 'ukbench00004.jpg', 'ukbench00005.jpg', 'ukbench00006.jpg', 'ukbench00007.jpg', 'ukbench00008.jpg', 'ukbench00009.jpg', 'ukbench00010.jpg', 'ukbench00011.jpg']
nbr_images=len(imlist)
featlist=[ imlist[i][:-3]+'sift' for i in range(nbr_images)]
"""for i in range(nbr_images):
sift.process_image(imlist[i], featlist[i])
"""
descr = []
descr.append(sift.read_features_from_file(featlist[0])[1])
descriptors = descr[0]
# sift.read_features_from_file(featlist[i])[0]:
# list of [pixel coord of each feature point, scale, rotation angle] for i-image
# size: (# of feature point x 4) for i-th image
#
# sift.read_features_from_file(featlist[i])[1]:
# list of [feature values] for i-th image
# size: (# of feature point x 128) for i-th image
for i in arange(1, nbr_images):
descr.append(sift.read_features_from_file(featlist[i])[1])
descriptors = vstack((descriptors, descr[i])) # stack of vector
#len(descr[0]): number of feature points -> 2276
#len(descr[0][1]): size of 1st feature vector -> 128
voc, distortion = kmeans(descriptors[::10,:],3,1) # select one per 10 rows, 3개의 word를 뽑아냄
len(voc) #3, voc = 3x128
len(voc[0]) #3
len(voc[1]) #128
nbr_words = voc.shape[0] #3
# (# of images, bins of histogram(= # of words))
# = (12x3)
imwords=zeros((nbr_images, nbr_words))
print imwords
words, distance = vq(descr[0],voc) # vector quantization
# len(words)->2276
# words: index vector of the cluster that each feature involves
# [1, 2, 1, 0, 1, 2, ...]
#voca = vocabulary.Vocabulary('ukbenchtest')
for i in range(nbr_images): # def project
hist = zeros((nbr_words))
words, distance = vq(descr[i],voc)
# 현재 im에 대해 각 feature가 속하는 word의 index와 이 word까지의 거리가 리턴
# index를 이용하여 해당 word에 보팅하여 histogram을 만듬
for w in words:
hist[w] += 1
imwords[i] = hist
print imwords # degree that each im involve to each cluster
"""
0 1 2 : cluster index (word가 3개이니까 index는 2까지)
[[ 766. 461. 1049.]: 1st image의 histogram의 모양
[ 725. 451. 1020.]: 2nd image의 "
[ 671. 461. 1133.]: ...
[ 1101. 630. 1403.]
[ 260. 317. 409.]
[ 267. 308. 370.]
[ 283. 394. 476.]
[ 239. 331. 410.]
[ 1105. 468. 1317.]
[ 116. 191. 390.]
[ 122. 251. 439.]
[ 1183. 597. 1475.]]: 12번째 im의 histogram모양
12번째 이미지의 모든 특징 중에서 word 0에 속하는 것은 1183개, 1번 597개, 2번 1475개이다. 3경우 합하면 특징의 개수이다. 따라서 test영상의 특징에 대한 histogram을 그리고 위 12개 중에서 hist모양이 비슷한 것을 찾으면 그것이 해당 영상이다.
"""







다음의 코드에서 voc의 내용을 알 수 있음.
2014년 8월 17일 일요일
Blog Visited
[Unit test]
C++ 프로젝트에 단위 테스트 도입하기
http://www.slideshare.net/mobile/zone0000/c-7522148
stinkfist : 구글테스트 시작하기
http://stinkfist.egloos.com/m/2262578
Rebooting Reiot
http://reiot.com/2008/07/04/google-test/
googletest 환경 구축 :: moltak
http://moltak.tistory.com/m/post/295
[LSH]
다음 블로그 NLP: http://blog.daum.net/hazzling?bz=blog
LSH(locality sensitive hashing)
GibHub로 이사: http://dsindex.github.io/
[DreamPark]
Windows Embeded 8.1 Industry Pro 리뷰:
http://ccami.tistory.com/92
MS dreampark에서 대학계정 무료 배포
[SWIG]
SWIG Tutorial
http://ppiazi.tistory.com/m/post/entry/SWIG-Tutorial#
C/C++ Wrapping에 의한 Tcl, Perl, Python, Java, C# 함수 제공
[SQLite]
SQLite 와 C++ 연동방법 :: 인생의무한루프
http://mins79.tistory.com/entry/SQLite-%EC%99%80-C-%EC%97%B0%EB%8F%99%EB%B0%A9%EB%B2%95
수까락의 프로그래밍 이야기 : SQLite - 튜토리얼 with CppSQLite
http://sweeper.egloos.com/m/3053076
CppSQLite - C++ Wrapper for SQLite - CodeProject
[Consumer Camera]
[usb3 Camera]
Buy e-con's Camera Boards | Camera Modules | Computer on Modules | Reference designs
http://www.e-consystems.com/webstore.asp
[Graphics Models]
Classical Probabilistic Models and Conditional Random Fields
http://www.scai.fraunhofer.de/fileadmin/images/bio/data_mining/paper/crf_klinger_tomanek.pdf
Machine Learning: Generative and Discriminative Models
http://www.cedar.buffalo.edu/~srihari/CSE574/Discriminative-Generative.pdf
[MCMC]
Sampling and MCMC (intractable integral)
http://arongdari.tistory.com/m/post/62#
Sampling and Markov Chain Monte Carlo
http://www.stat.cmu.edu/~larry/=sml2008/lect2.pdf
Toy code
http://www.ece.sunysb.edu/~zyweng/MCMCexample.html
Monte Carlo Methods
http://www.cs.cmu.edu/~ggordon/MCMC/
Impacted paper
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.13.7133&rep=rep1&type=pdf
Sampling & MCMC
http://arongdari.tistory.com/m/post/entry/Sampling-MCMC#
[L1-Regularized Min]
Parallel Coordinate Descent for L1-Regularized Loss Minimization
http://www.select.cs.cmu.edu/publications/paperdir/icml2011-bradley-kyrola-bickson-guestrin.pdf
[GoPro Hero4 Livestream]
http://www.reddit.com/r/gopro/comments/2md8hm/how_to_livestream_from_a_gopro_hero4/
OpenCV in C++
https://gist.github.com/KonradIT/8554673
#include <opencv2/opencv.hpp>
int main()
{
cv::VideoCapture cap( "http://10.5.5.9:8080/live/amba.m3u8" );
cv::namedWindow( "GoPro" );
cv::Mat frame;
do {
cap >> frame;
cv::imshow( "GoPro", frame );
} while ( cv::waitKey( 30 ) < 0 );
return 0;
}
C++ 프로젝트에 단위 테스트 도입하기
http://www.slideshare.net/mobile/zone0000/c-7522148
stinkfist : 구글테스트 시작하기
http://stinkfist.egloos.com/m/2262578
Rebooting Reiot
http://reiot.com/2008/07/04/google-test/
googletest 환경 구축 :: moltak
http://moltak.tistory.com/m/post/295
[LSH]
다음 블로그 NLP: http://blog.daum.net/hazzling?bz=blog
LSH(locality sensitive hashing)
GibHub로 이사: http://dsindex.github.io/
[DreamPark]
Windows Embeded 8.1 Industry Pro 리뷰:
http://ccami.tistory.com/92
MS dreampark에서 대학계정 무료 배포
[SWIG]
SWIG Tutorial
http://ppiazi.tistory.com/m/post/entry/SWIG-Tutorial#
C/C++ Wrapping에 의한 Tcl, Perl, Python, Java, C# 함수 제공
[SQLite]
SQLite 와 C++ 연동방법 :: 인생의무한루프
http://mins79.tistory.com/entry/SQLite-%EC%99%80-C-%EC%97%B0%EB%8F%99%EB%B0%A9%EB%B2%95
수까락의 프로그래밍 이야기 : SQLite - 튜토리얼 with CppSQLite
http://sweeper.egloos.com/m/3053076
CppSQLite - C++ Wrapper for SQLite - CodeProject
MFC + SQLite3 연동 :: 개발환경을 만들자
[運]과 함께하는 세상 : SQLite 와 C++ 연동방법
SQLite 쿼리 간단 사용법 매뉴얼 기본 동작 상세 설명 :: 포쿠테
[Matlab]
MATLAB 때려잡기 - 01강 - Modern Control Theory 때려잡기 - What is Control Theory?
[Consumer Camera]
범용 카메라를 이용한 이미지 처리: Nikon Imaging | SDK Download
[usb3 Camera]
http://www.e-consystems.com/webstore.asp
[Graphics Models]
Classical Probabilistic Models and Conditional Random Fields
http://www.scai.fraunhofer.de/fileadmin/images/bio/data_mining/paper/crf_klinger_tomanek.pdf
Machine Learning: Generative and Discriminative Models
http://www.cedar.buffalo.edu/~srihari/CSE574/Discriminative-Generative.pdf
discriminative vs. generative, classification vs. categorization
[MCMC]
Sampling and MCMC (intractable integral)
http://arongdari.tistory.com/m/post/62#
Sampling and Markov Chain Monte Carlo
http://www.stat.cmu.edu/~larry/=sml2008/lect2.pdf
Toy code
http://www.ece.sunysb.edu/~zyweng/MCMCexample.html
Monte Carlo Methods
http://www.cs.cmu.edu/~ggordon/MCMC/
Impacted paper
http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.13.7133&rep=rep1&type=pdf
Sampling & MCMC
http://arongdari.tistory.com/m/post/entry/Sampling-MCMC#
[L1-Regularized Min]
Parallel Coordinate Descent for L1-Regularized Loss Minimization
http://www.select.cs.cmu.edu/publications/paperdir/icml2011-bradley-kyrola-bickson-guestrin.pdf
[GoPro Hero4 Livestream]
The new HERO4 Black and Silver edition cameras use a different, more powerful chip (ambarella A9). The traditional URL for HERO2/HERO3/HERO3+ http://10.5.5.9:8080/live/amba.m3u8 does not work for the new HERO4 camera.
Here is how to get the live stream:
- Open this URL: http://10.5.5.9/gp/gpExec?p1=gpStreamA9&c1=restart
- In VLC/FFplay/other open the udp port: udp://:8554
- Make sure the media player is configured as mpeg streaming.
http://www.reddit.com/r/gopro/comments/2md8hm/how_to_livestream_from_a_gopro_hero4/
OpenCV in C++
https://gist.github.com/KonradIT/8554673
#include <opencv2/opencv.hpp>
int main()
{
cv::VideoCapture cap( "http://10.5.5.9:8080/live/amba.m3u8" );
cv::namedWindow( "GoPro" );
cv::Mat frame;
do {
cap >> frame;
cv::imshow( "GoPro", frame );
} while ( cv::waitKey( 30 ) < 0 );
return 0;
}
2014년 8월 12일 화요일
Path planning of mobile robot
작성 중...
$V(t)$와 $\omega(t)$는 control input.
로봇의 시작 점과 목표 점이 주어진다고 할 때,
Path는 $P(u)$에 의해 정의된다. 파라메터인 $u$는 0에서 1까지 변하는 값으로 0은 로봇의 시작 점, 1은 목표 점을 가리킨다.
이 수식은 아주 많은 파라메터들로 구성되는데 이 값들을 바꾸면 다양한 형태의 path가 생성된다 [1].
만일 장애물을 회피하여 목표 점까지 이동한다 가정하자. 경로는 시작 위치에서 장애물을 피하고 목표 위치로 부드럽게 수렴하는 경로를 얻는 것이 필요하다.
여러 파라메터 중에서 2개의 파라메터를 고려하면,
$Path=f(\eta_3, \theta_a)$
이고 path는 다양한 파라메터 중에서 두 변수가 중요하게 작용하므로 이들의 함수이다.
현재 로봇이 가진 각도를 기준으로 전방 180도로 정의하면,
$\theta_a$를 0~180에서 10도씩 나누고, 각 $\theta$에 대해 10개의 $\eta$를 정의한다.
그러면 위 그림의 상부와 같은 경로들이 나온다.
즉, 10도씩 나누어 19개의 set가 있고, 각 set 내에는 ($\eta$의 변화에 따라) 10개의 path가 존재한다.
이렇게 정의한 여러 path 중에서 최적인 하나를 선정하는 것이 필요하다.
로봇은 자체 회전이 가능하여 어떤 출발 각도를 가지고도 출발할 수 있다.
이동 경로 길이가 짧으면서 장애물 충돌 없이 목표에 도달하는 것이 필요하다.
예를 들면 출발 각이 목표 각과 비슷하면 경로 길이는 짧아 진다.
경로를 결정하였으면 로봇이 경로를 따라 잘 이동하도록 제어하는 것이 필요하다.
current 위치에서 destination으로 위치와 자세를 바꾸기 위해서 오차를 위 행렬 식처럼 정의한다.
Lyapunov함수를 이용하여 비용함수 $V$를 정의한다. 식을 보면 $x_e, y_e, \theta_e$가 모두 0으로 가면 $V$도 0으로 수렴한다.
References
[1] Lyapunov Theory
Online boosting
초기에 지정된 영역을 5개 부분으로 나누어 (+1/-1)로 학습.
물체 추적 시에는 물체 크기의 window를 sliding시켜 ROI 내부를 검색.
현재 위치에 대해 window 내부의 특징을 classifier로 평가하고 confidence 계산.
ROI 내부의 confidence map를 저장하고, map에 대해 integral image를 적용시켜 최대 confidence 영역을 찾아 냄.
최대 영역이 새로운 물체의 위치(+)가 되고, 이 물체의 배경(-)과 함께 다시 학습(update).
2014년 8월 4일 월요일
영상 특징에 대한 이해
작성 중....
물체 검출(object detection)은 머신비전에서 가장 중요한 주제 중의 하나이다. 물체 검출의 실행에 있어 물체를 포함하는 입력 데이터나 영상 정보를 그대로 사용하지 않고 재구성을 요구한다. 재구성된 특징의 구별성이 더 좋을수록 더 간단한 학습과 분류가 가능하다. 따라서 입력 데이터를 재구성하는 것은 대단히 중요하다. 보통 입력 영상의 픽셀 밝기를 직접적으로 이용하지는 않고, 대신 밝기나 카메라가 물체를 찍은 주시점, 형상, 외관, 자세변화에 불변하는 영상 표현이 요구된다.
물체 검출을 위해 다양한 영상특징이 개발되었고 그중 HOG, Haar 웨이브릿, LBP, BoW, SIFT등이 대표적인 영상 특징이다. 여기서는 일반적으로 널리 사용되는 몇 가지 특징에 대해 분석하고 이러한 특징이 분류기에 사용되었을 경우, 학습 성능, 계산량, 분류성능 등의 비교를 통해 가장 적합한 특징을 선정하고 본 연구에서 목표로 하는 물체 인식에 이용하기 위한 토대를 마련한다.
➀ LBP 적용 연구
Local Binary Pattern(LBP)은 단순하지만 강력한 영상 텍스춰 묘사자(texture descriptor)이다. LBP는 텍스춰 패턴을 정량화하며 자세나 크기, 밝기 변화에 강인한 특징을 보인다. 또한 계산이 단순하여 실시간 처리 작업에 적당하다. 적용 분야는 얼굴이나 표정인식, 물체 인식, 배경추출, 자세나 응시 게이트 인식 등이다. 영상에서 어떤 픽셀의 LBP는 이 픽셀의 밝기 값과 이웃 밝기 값을 비교함에 의해 생성되는 일련(series)의 이진수이다. 이웃 반경의 크기나 이웃 픽셀의 수는 자유롭게 선택 가능하다. 이진수 계산은 중심 픽셀과 이웃 픽셀 값을 비교하는 것으로 만일 이웃 픽셀 값이 더 커면 이진수는 1, 그렇지 않으면 0이다.
물체 검출(object detection)은 머신비전에서 가장 중요한 주제 중의 하나이다. 물체 검출의 실행에 있어 물체를 포함하는 입력 데이터나 영상 정보를 그대로 사용하지 않고 재구성을 요구한다. 재구성된 특징의 구별성이 더 좋을수록 더 간단한 학습과 분류가 가능하다. 따라서 입력 데이터를 재구성하는 것은 대단히 중요하다. 보통 입력 영상의 픽셀 밝기를 직접적으로 이용하지는 않고, 대신 밝기나 카메라가 물체를 찍은 주시점, 형상, 외관, 자세변화에 불변하는 영상 표현이 요구된다.
물체 검출을 위해 다양한 영상특징이 개발되었고 그중 HOG, Haar 웨이브릿, LBP, BoW, SIFT등이 대표적인 영상 특징이다. 여기서는 일반적으로 널리 사용되는 몇 가지 특징에 대해 분석하고 이러한 특징이 분류기에 사용되었을 경우, 학습 성능, 계산량, 분류성능 등의 비교를 통해 가장 적합한 특징을 선정하고 본 연구에서 목표로 하는 물체 인식에 이용하기 위한 토대를 마련한다.
➀ LBP 적용 연구
Local Binary Pattern(LBP)은 단순하지만 강력한 영상 텍스춰 묘사자(texture descriptor)이다. LBP는 텍스춰 패턴을 정량화하며 자세나 크기, 밝기 변화에 강인한 특징을 보인다. 또한 계산이 단순하여 실시간 처리 작업에 적당하다. 적용 분야는 얼굴이나 표정인식, 물체 인식, 배경추출, 자세나 응시 게이트 인식 등이다. 영상에서 어떤 픽셀의 LBP는 이 픽셀의 밝기 값과 이웃 밝기 값을 비교함에 의해 생성되는 일련(series)의 이진수이다. 이웃 반경의 크기나 이웃 픽셀의 수는 자유롭게 선택 가능하다. 이진수 계산은 중심 픽셀과 이웃 픽셀 값을 비교하는 것으로 만일 이웃 픽셀 값이 더 커면 이진수는 1, 그렇지 않으면 0이다.
그림 1. LBP 연산 과정
예를 들어, 3x3픽셀영역에서 LBP를 계산하면 그림 1에 표현된다. 중심 픽셀 값 5와 함께 주위 값을 비교함에 의해 이진 값들이 얻어진다. 주어진 예제에서 얻어진 이진 값은 좌측 중심을 시작점으로 반시계 방향으로 회전 했을 때 01101011이다. 이때, 이진 값에 가중치를 보태어 하나의 숫자로 만든다. 가중치는 2의 배수로 할당되고 주어진 이진 코드에 대한 값은 1+2+8+32+64=107이다. 어떤 픽셀의 LBP 코드 값은 다음과 같은 식으로 주어진다.
$LBP_{P,R}=\sum_{p=0}^{P-1}s(g_p-g_c) \cdot 2^p$
$s(x)=\begin{cases} 1, if \space x \ge 0\\ 0, otherwise\end{cases}$
상기한 수식 에서 P는 이웃 픽셀의 수이고, gp와 gc는 이웃 픽셀과 중심 픽셀의 밝기 값이다. 이웃은 그림 2과 같이 원형이나 사각형으로 구성할 수 있으며, 패턴의 출발점은 미리 정해진다. 일단 P와 R이 정해지면, LBP는 만들어진다.
$LBP_{P,R}=\sum_{p=0}^{P-1}s(g_p-g_c) \cdot 2^p$
$s(x)=\begin{cases} 1, if \space x \ge 0\\ 0, otherwise\end{cases}$
상기한 수식 에서 P는 이웃 픽셀의 수이고, gp와 gc는 이웃 픽셀과 중심 픽셀의 밝기 값이다. 이웃은 그림 2과 같이 원형이나 사각형으로 구성할 수 있으며, 패턴의 출발점은 미리 정해진다. 일단 P와 R이 정해지면, LBP는 만들어진다.
그림 3은 텍스춰를 정의하기 위해 선택한 P와 R의 세 가지 다른 값을 보여준다. LBP는 쉽게 계산되지만 위치에 매우 민감하기 때문에 그대로 사용하기는 어렵다. 위치가 달라지면 오차가 매우 커진다. 따라서 실용적 사용을 위해 많은 수의 LBP 특징을 포함하는 어떤 셀(cell)에 대한 LBP 히스토그램(histogram)을 만들 필요가 있다.
요약하면, LBP 특징 벡터는 다음 단계로 만들어 진다.
1 (1) 히스토그램이 만들어질 셀의 크기를 결정한다(예를 들면 16x16). 그리고 현재 윈도를 셀들로 분할한다.
(2) 셀 내의 픽셀들에 대해 LBP 패턴을 계산한다. 패턴의 출발점과 회전 방향을 정의하고 중심 픽셀과 이웃 픽셀을 비교하여 중심픽셀의 패턴 값을 얻는다.
(3) 각 셀의 히스토그램을 계산한다. 즉, 이진 패턴이 나타내는 숫자의 발생 빈도를 얻는다.
(4) 선택적으로 히스토그램을 정규화하거나 모든 셀의 정규화 된 히스토그램을 연결하여 현재의 탐색 윈도를 표현한다.
➁ BoW
BoW(Bag of Words)는 전산학의 자연어 처리(natural language processing) 분야에서 시작되어 Visual한 요소를 다룰 수 있도록 응용되어 Bag of Visual Words란 이름으로 머신비전 분야에서 널리 사용되고 있는 영상 분류 기법 중에 하나이다.
Bag이란 문서에서 반복되어 나타나는 단어나 영상에서 반복되어 보이는 패턴들의 집합이다. 문장에서 생각해 보면, 단어순서나 문법은 무시되고 문서는 단순히 단어들의 집합으로 표현된다. BoW는 문장에서 나타나는 항목(entry)의 발생빈도를 표현한다. 이때 사용되는 사전(dictionary)이란 항목들의 집합으로 문장 내에서 나타나는 모든 단어들로 만들어 진다.
예를 들어, 다음과 같은 두개의 문장이 있다고 가정하자:
문장 1: Mary likes to play volleyball. John likes too.
문장 2: Mary also likes to play basketball.
이때 사전은 다음과 같다:
{1: Mary, 2: like, 3: to, 4: play, 5: volleyball, 6: John, 7: too, 8: also, 9: basketball}
최종적으로 두 문장은 사전의 항목 인덱스들의 발생빈도로 표현된다. 아래는 두 문장의 BoW이다.
문장 1: [1 2 1 1 1 1 1 0 0]
문장 2: [1 1 1 1 0 0 0 1 1]
BoW의 개념을 영상인식 분야에 적용한다면, 영상은 문장에 대응되고 단어들의 Bag은 그림 4에서 보이는 영상의 부분 특징들을 표현한다. BoW에 대응되는 Bag of visual words는 이러한 부분 영상 특징들의 사전 내 항목의 발생 빈도 값의 벡터가 된다. 가장 많이 사용되는 부분 영상 특징 중의 하나는 SIFT이다. SIFT는 물체의 크기, 밝기, 어파인 변화에도 특징 값이 불변하는 신뢰성을 가진다.
BoW의 절차는 항목 생성(Vocabulary Generation)과 영상 표현(Image Representation)으로 나누어 아래 그림 5와 같이 수행된다.
Vocabulary generation:
1) Extract SIFT feature of all training images.
2) Cluster the SIFT features extracted in Step 1 to a pre-defined groups (such as 300 groups) by K-means algorithm and express each cluster as a "center features" compose the vocabulary.
Image representation:
3) Extract SIFT feature of the image that is required to be represented.
4) Calculate the Euclidean between the SIFT features acquired in Step 3 and each entry of the vocabulary, and label each feature by the vocabulary index with the smallest distance.
5) Create the histogram of indexes that were achieved in Step 4, and this histogram is the BoW of the image.
그림 5. BoW 과정
본 연구에서는 먼저 사람의 학습 영상에 대해 SIFT를 적용하여 사전을 구성한다. 사전의 엔트리는 전부 30개(즉, 특징 값의 K-means 클러스터링 후에 얻어진 중심 특징의 개수)로 한다.
학습 영상이 주어지면 먼저 영상을 8x8 크기의 패치로 분할한다. 각각의 패치에 대해 SIFT특징을 하나 추출한다. 이 특징으로 30개의 사전 엔트리와 유클리디안 거리 30개를 얻는다. 이 거리 값의 역(inverse)을 취해 30개의 값을 가진 벡터 하나를 구성한다. 학습 영상의 모든 패치에 대해 벡터를 추출하면 패치의 개수만큼 벡터가 생기게 된다. 학습 영상의 개수는 아주 많으므로 벡터의 개수는 매우 많다. Positive 학습영상과 Negative 학습영상에 대해 이 벡터들을 추출하여 SVM을 학습한다.
요약하면, LBP 특징 벡터는 다음 단계로 만들어 진다.
1 (1) 히스토그램이 만들어질 셀의 크기를 결정한다(예를 들면 16x16). 그리고 현재 윈도를 셀들로 분할한다.
(2) 셀 내의 픽셀들에 대해 LBP 패턴을 계산한다. 패턴의 출발점과 회전 방향을 정의하고 중심 픽셀과 이웃 픽셀을 비교하여 중심픽셀의 패턴 값을 얻는다.
(3) 각 셀의 히스토그램을 계산한다. 즉, 이진 패턴이 나타내는 숫자의 발생 빈도를 얻는다.
(4) 선택적으로 히스토그램을 정규화하거나 모든 셀의 정규화 된 히스토그램을 연결하여 현재의 탐색 윈도를 표현한다.
➁ BoW
BoW(Bag of Words)는 전산학의 자연어 처리(natural language processing) 분야에서 시작되어 Visual한 요소를 다룰 수 있도록 응용되어 Bag of Visual Words란 이름으로 머신비전 분야에서 널리 사용되고 있는 영상 분류 기법 중에 하나이다.
Bag이란 문서에서 반복되어 나타나는 단어나 영상에서 반복되어 보이는 패턴들의 집합이다. 문장에서 생각해 보면, 단어순서나 문법은 무시되고 문서는 단순히 단어들의 집합으로 표현된다. BoW는 문장에서 나타나는 항목(entry)의 발생빈도를 표현한다. 이때 사용되는 사전(dictionary)이란 항목들의 집합으로 문장 내에서 나타나는 모든 단어들로 만들어 진다.
예를 들어, 다음과 같은 두개의 문장이 있다고 가정하자:
문장 1: Mary likes to play volleyball. John likes too.
문장 2: Mary also likes to play basketball.
이때 사전은 다음과 같다:
{1: Mary, 2: like, 3: to, 4: play, 5: volleyball, 6: John, 7: too, 8: also, 9: basketball}
최종적으로 두 문장은 사전의 항목 인덱스들의 발생빈도로 표현된다. 아래는 두 문장의 BoW이다.
문장 1: [1 2 1 1 1 1 1 0 0]
문장 2: [1 1 1 1 0 0 0 1 1]
BoW의 개념을 영상인식 분야에 적용한다면, 영상은 문장에 대응되고 단어들의 Bag은 그림 4에서 보이는 영상의 부분 특징들을 표현한다. BoW에 대응되는 Bag of visual words는 이러한 부분 영상 특징들의 사전 내 항목의 발생 빈도 값의 벡터가 된다. 가장 많이 사용되는 부분 영상 특징 중의 하나는 SIFT이다. SIFT는 물체의 크기, 밝기, 어파인 변화에도 특징 값이 불변하는 신뢰성을 가진다.
BoW의 절차는 항목 생성(Vocabulary Generation)과 영상 표현(Image Representation)으로 나누어 아래 그림 5와 같이 수행된다.
Vocabulary generation:
1) Extract SIFT feature of all training images.
2) Cluster the SIFT features extracted in Step 1 to a pre-defined groups (such as 300 groups) by K-means algorithm and express each cluster as a "center features" compose the vocabulary.
Image representation:
3) Extract SIFT feature of the image that is required to be represented.
4) Calculate the Euclidean between the SIFT features acquired in Step 3 and each entry of the vocabulary, and label each feature by the vocabulary index with the smallest distance.
5) Create the histogram of indexes that were achieved in Step 4, and this histogram is the BoW of the image.
그림 5. BoW 과정
본 연구에서는 먼저 사람의 학습 영상에 대해 SIFT를 적용하여 사전을 구성한다. 사전의 엔트리는 전부 30개(즉, 특징 값의 K-means 클러스터링 후에 얻어진 중심 특징의 개수)로 한다.
학습 영상이 주어지면 먼저 영상을 8x8 크기의 패치로 분할한다. 각각의 패치에 대해 SIFT특징을 하나 추출한다. 이 특징으로 30개의 사전 엔트리와 유클리디안 거리 30개를 얻는다. 이 거리 값의 역(inverse)을 취해 30개의 값을 가진 벡터 하나를 구성한다. 학습 영상의 모든 패치에 대해 벡터를 추출하면 패치의 개수만큼 벡터가 생기게 된다. 학습 영상의 개수는 아주 많으므로 벡터의 개수는 매우 많다. Positive 학습영상과 Negative 학습영상에 대해 이 벡터들을 추출하여 SVM을 학습한다.
Bayes Theory를 이용한 도로 영상 분할
식 (1)에서 부류를 나타내는 $X$는
차선($L$), 도로($P$), 물체($O$), 기타($U$)의 4가지이다. $X=[L, P, O, U]$이다. Given $z$(측정값, 즉 어떤 하나의 픽셀이 주어졌을 때)에서 사후 확률(이 픽셀이 4가지의 부류 중에서 어디에 속할지를 나타내는 $X$를 결정하는)을 바로 계산할 수가 없기 때문에 베이스 이론을 적용하여
우도(likelihood)와 사전 확률(prior)을 통해
계산하고자 한다.
$p(X|z) = {p(z|X)p(X) \over p(z)}$ (1)
(1) 우도의
계산
우도는 $p(z|X)$이고 우도 계산에 사용할 측정 데이터는 2가지가 존재한다. 하나는 원 이미지(흑백 이미지) 데이터에서 나온 확률 분포이다.
$p(i|X)$ (2)
다른 하나는 차선추출을 위해 적용한 모폴로지 필터가 적용된 결과 영상에서 나온 분포이다.
$p(L|X)$ (3)
그런데 두 데이터의 측정은 서로 독립적이다. 따라서
$p(z|X)
= p(i|X)p(L|X)$ (4)
이다. 이제
남은 문제는 $p(i|X)$와 $p(L|X)$의 결정이다. 서로 관계가 없으므로 $p(i|X)$만 따로 결정해 보고, 이 방법을 $p(L|X)$를 결정하는데 그대로 사용한다.
$p(i|X)$에서 부류 $X$는 4가지이고, 각각의 부류는 정규분포(normal
distribution)을 가진다고 가정하자. 그러면 $p(i|X)$는 4가지의 부류가 서로 합성된 분포, 즉 Gaussian분포 4개가 섞인 혼합모델이 된다. 즉 Gaussian Mixture Model(GMM)이다.
따라서 지금부터 문제는 GMM 분포의
4개의 분포를 결정하는 문제가 된다. 4개의 분포는 8개의
파라메타를 가진다. 평균 4개와 분산 값 4개이다. 즉, 주어진
데이터를 사용하여 8개의 파라메타를 결정해야 한다. 데이터는 픽셀의 밝기 값이다. 원 영상을 평면 변환(plane
homography)한 영상의 각 픽셀에 대해 이 픽셀이 4개의 부류 중에서 어디에 속할
것 인지와 이 소속도를 가지고 각 부류의 평균, 분산을 계산하여야 한다.
GMM 모델은
EM(Expectation and Maximization) 알고리즘을 이용하여 풀어지는데 EM 알고리즘은
먼저 이미지 내의 각 픽셀이 4개의 부류 중에서 어디에 속할 것인지의 소속 확률을 가정한다.
초기에 아무 지식이 없다면 어떤 픽셀이 0.25의 크기로 각 분포에
속한다고 가정할 수 있다(E 단계).
다음 이 소속도를 사용하여 4가지 분포의 평균, 분산, 각 분포의 가중치 파라메터 값들을 계산한다 (M 단계).
이 값들을 사용하면 다시 각 픽셀들의 4가지 분포에 대한 소속도를
갱신하는 것이 가능하다(다시 E 단계).
소속도가 갱신 되었으니 다시 평균, 분산, 가중치의 갱신이 가능하다(다시 M
단계).
이러한 과정을 반복하고 수렴하면 각 픽셀이 4가지 부류의 어디에 속하는지를
정확하게 계산하는 것이 가능하다. 파라메터를 모두 얻으면 $p(i|X)$값이 GMM 모델로서 완전하게 결정된다.
이러한 과정을 $p(L|X)$에 대해서도 동일하게 적용하면 $p(L|X)$의 파라메터들을 얻는 것도 가능하다.
그런데 EM 알고리즘의 보다 정확한 수렴을 위해서는 초기 값을 잘
설정해야 하는데 논문에서는 각 픽셀의 초기 소속도를 얻기 위한 전처리 기법이 나와 있다. 잘 분할된
초기 값에서 출발하면 정확한 파라메터를 쉽게 얻을 것이다.
(2)
prior 확률 $p(X)$를 계산
우도를 결정하였으므로 Bayes 식 적용을 위해서는 사전 확률 $p(X)$를 계산하여야 한다. 그런데 도로 영상은 차량에 설치된 카메라에서
볼 때 시간 축에서 비슷한 영상이 연속적으로 취득된다. 두 연속 영상은 비슷하다. 따라서 $p(X)$는 이전 영상의 사후 확률을 다음 단계의 사전 확률로
그대로 사용해도 무관하다.
첫 프레임에는 사전 확률은 균일하게 두고 사용할 수 있을 것이다. 또, 터널 진출입과 같이 밝기
분포가 급격하게 바뀌는 경우만 따로 취급할 수 있다(논문 참조).
우도와 사전 확률이 모두 결정되었으면 Bayes 모델을 새로운 Test 영상에 대해 적용한다. Test 영상 내의 각 픽셀 측정치 $z_i$의 밝기 값 $I_i$와 필터링 값 $L_i$는 Bayes 모델에 적용되고 $p(X_p|z_i)$, $p(X_L|z_i)$, $p(X_o|z_i)$, $p(X_u|z_i)$를 계산 후 가장 큰 확률을 가진 부류에 이 픽셀을 할당한다.
References
[1] M. Nieto et.
al., Road environment modeling using robust perspective analysis and recursive
Bayesian segmentation, Machine Vision and Applications, 2011.
2014년 7월 21일 월요일
POP3와 IMAP
IMAP: 메일 서버와 메일관리 시스템(outlook 등)이 동기화되어 동작.
POP3: Outlook에서 서버에 접근해서 다운 받은 후, 서버의 메일을 제거.
설정 방법: 제어판->메일->전자메일계정->새로만들기->계정유형(POP3 or IMAP 선정)
POP3와 IMAP를 둘 다 만들고 이 중 하나를 "기본"으로 선택
.기본설정 메일 이외에는 데이터 제거 가능
.기본설정 메일의 옵션 중에 서버 메일 제거전 잔류 시간 설정가능(POP3의 경우)
그리고 새로 도착/보내는 메일이 저장되는 파일을 지정하기 위해서
제어판->모든 제어판 항목->메일(32비트)->전자메일계정->폴더변경을 클릭 후 "새 Outlook 데이터 파일"에서 데이터 파일을 옮긴 디렉토리의 파일을 선택해서 등록 필요.
**아이폰에서 메일 설정 시에 서버에 메일 남겨놓아도 일주일 후에 자동 삭제하는 기능이 있으므로 Gmail 같은곳에서 메일 가져갈 때 남겨놓으면 됨.
POP3: Outlook에서 서버에 접근해서 다운 받은 후, 서버의 메일을 제거.
설정 방법: 제어판->메일->전자메일계정->새로만들기->계정유형(POP3 or IMAP 선정)
POP3와 IMAP를 둘 다 만들고 이 중 하나를 "기본"으로 선택
.기본설정 메일 이외에는 데이터 제거 가능
.기본설정 메일의 옵션 중에 서버 메일 제거전 잔류 시간 설정가능(POP3의 경우)
그리고 새로 도착/보내는 메일이 저장되는 파일을 지정하기 위해서
제어판->모든 제어판 항목->메일(32비트)->전자메일계정->폴더변경을 클릭 후 "새 Outlook 데이터 파일"에서 데이터 파일을 옮긴 디렉토리의 파일을 선택해서 등록 필요.
**아이폰에서 메일 설정 시에 서버에 메일 남겨놓아도 일주일 후에 자동 삭제하는 기능이 있으므로 Gmail 같은곳에서 메일 가져갈 때 남겨놓으면 됨.
2014년 6월 24일 화요일
DPM: Octave in HOG feature
Object detection에서 HOG(Histogram of Oriented Gradients) 특징의 사용은 많은 응용분야에서 일반화 되었다. DPM에서도 HOG특징을 사용하고 있는데, 원래 HOG가 제안될 때는 128차원 vector를 사용하였다. DPM에서는 원래의 HOG에 Eigen analysis를 도입하여 31차원으로 특징공간을 줄인 HOG를 사용하고 있다.
아래에 주어진 코드는 DPM에서 사용하는 HOG특징에 대한 것이다. 주어진 영상(여기서는 480x640 pixels)에 대해 다수의 Octave를 구축하여 특징을 얻는다.
관심 물체(사람, 자전거, 자동차, ...)는 카메라와 물체 사이의 거리에 따라 영상 내에서 크기가 달라질 수 있다. 따라서, 모델 크기와 비교하여 달라질 수 있는 다양한 scale에 대해 물체 탐색(일반적으로 sliding window search을 사용)을 수행해야 한다.
다양한 스케일에 대해 물체를 탐색하기 위해 image pyramid를 사용할 수 있다. 먼저, 다양한 영상 크기를 만들고, 각각의 영상에 대해 HOG 특징 값을 추출하여 사용한다.
먼저 테스트할 영상을 입력한다.
>> im=imread('000034.jpg');
함수를 호출하여 특징을 추출한다. 10개의 octave를 구축한다. HOG 특징을 계산할 cell의 크기는 8 pixels을 사용한다.
DPM에서는 HOG를 coarse level과 fine level로 나누어 사용하는데, coarse level에서는 8x8 pixels patch에 대해 HOG를 추출하여 사용하며, fine level은 4x4 pixels patch에서 HOG를 추출하여 사용한다.
추출 순서는 먼저 coarse level에서 8x8 HOG에 의한 물체의 개략적 윤곽(외곽)을 이용하여 물체가 있을 수 있는 위치를 추출하고, 추출된 후보 위치에서 물체를 구성하는 part를 인식할 때는 fine level의 HOG를 사용한다.
>> [feat, scale] = featpyramid(im, 8, 10); % octave내의 스케일 수 = 10
>> size(feat)
ans =
46 1 % 전체 이미지 피라미드는 46단계로 구성
>> size(feat{1}) % 첫번째 영상 특징은 480x640 pixels 영상 크기에 대해
% 118x158개의 31차원 특징 벡터(4x4 cell HOG)가 얻어졌다.
ans =
118 158 31
>> size(scale)
ans =
46 1
function [feat, scale] = featpyramid(im, sbin, interval)
% [feat, scale] = featpyramid(im, sbin, interval);
% Compute feature pyramid.
%
% sbin is the size of a HOG cell - it should be even.
% interval is the number of scales in an octave of the pyramid.
% feat{i} is the i-th level of the feature pyramid.
% scale{i} is the scaling factor used for the i-th level.
% feat{i+interval} is computed at exactly half the resolution of feat{i}.
% first octave halucinates higher resolution data.
sc = 2 ^(1/interval); % sc=1.0718
imsize = [size(im, 1) size(im, 2)]; % 480x640
max_scale = 1 + floor(log(min(imsize)/(5*sbin))/log(sc)); % 36
feat = cell(max_scale + interval, 1); % 46
scale = zeros(max_scale + interval, 1); % 46
% our resize function wants floating point values
im = double(im);
for i = 1:interval % 1~10
% i=1일 때, scaled=480x640x3(color)
% ~i=10이면, scaled=257x343x3까지 작아짐
scaled = resize(im, 1/sc^(i-1));
% "first" 2x interval
feat{i} = features(scaled, sbin/2); % 118x158x31(i=1),fine level hog
scale(i) = 2/sc^(i-1); % 2
% "second" 2x interval
feat{i+interval} = features(scaled, sbin); %58x78x31(i=1),coarese level
scale(i+interval) = 1/sc^(i-1);
% remaining interals
for j = i+interval:interval:max_scale % j=11,21,31(i=1)
scaled = resize(scaled, 0.5); %240x320x3(i=1,j=11)
feat{j+interval} = features(scaled, sbin); %28x38,31(i=1,j=11)
scale(j+interval) = 0.5 * scale(j); % 0.5
end
% i=1일 때의 iteration에 대해
% feat: 1, 11, (21, 31, 41)이 계산됨(단, 괄호는 j루프에서 계산)
% i=2이면, feat: 2, 12, (22, 32, 42)가 계산...
% i=3, feat: 3, 13, (23, 33, 43), ...
% i=6, feat: 6, 16, (26, 36, 46)
% i=7, feat: 7, 17, (27, 37)
% i=9, feat: 9, 19, (29, 39)
% i=10, feat: 10, 20, (30, 40)
% feat{1~10}까지는 4x4 cell크기의 hog 특징 저장
% 정리하면,
% feat: 1~10까지는 480x640에서 257x343까지 작아지는 10개의 영상에 대해
% 4x4cell hog를 적용하여 특징을 추출한 것
% feat: 11~20까지는 480x640 -> 257x343로 점차 작아지는 영상(10단계)에 대해
% 8x8cell hog를 적용하여 특징 추출
% feat: 21, 31, 41, 480x640을 계속 절반씩 줄이면서(320x240->160x120->80x60)
% 8x8cell을 적용하여 특징을 추출한 것
% feat: 22, 32, 42, 448x597을 계속 절반씩 줄이면서(224x298->...)
% 8x8cell을 적용하여 특징을 추출한 것
% feat: 23, 33, 43, 418x557을 계속 절반씩 줄이면서(209x278->...)
% 8x8cell을 적용하여 특징을 추출한 것
% ... feat: ...
%
% feat을 grouping하면(이것을 octave라고 함)
% 1(480x640,4x4cell),11(480x640,8x8cell),21(240x320,8x8cell),31((120x160,
% 8x8cell),41((60x80,8x8cell)
% 2(448x597,4x4cell),12(448x597,8x8cell),22(224x298,8x8cell),
% 32(112x149,8x8cell),42((56x74,8x8cell)
% ...
% octave가 10개가 생김
end
References
[1] Compiling matlab mex file in Windows 64bit and Matlab 2010a 64bit with VS10.0(VS2010).
관리자 권한으로 매트랩 실행. 압축을 풀기위함. 이후 매트랩 실행시에는 관리자 권한으로 실행할 필요 없음.
>>unzip('d:\temp_mat\S2010MEXSupport.zip', matlabroot); %Matlab 2010a에서 Visual Studio 10.0(VS2010) 컴파일러를 연동시키기 위한 패치파일
>>mex -setup % Visual Studio 10.0 컴파일러를 선택한다.
>>yprime(1,1:4) %실행되지 않는다.
>>mex c:\mex\yprime.c %현재 폴더에 yprime.mexw64 파일이 생성된다.
>>yprime(1, 1:4) %실행됨
참고사항: Visual Studio 2008 SP1은 64bit 컴파일러를 기본적으로 설치하지 않기 때문에 64비트 매트랩 환경에서는 컴파일이 안될수도 있다.
http://www.mathworks.co.kr/support/solutions/en/data/1-6IJJ3L/?solution=1-6IJJ3L
[2] resize.cc 컴파일 방법:
DPM의 소스 코드에 있는 resize.cc 파일에 대해 직접 컴파일 해 보니 몇 함수가 정의되지 않았다는 메시지가 나왔음. 따라서 아래와 같이 추가:
#define bzero(s,n) memset ((s), 0, (n))
#define round(x) (x<0?ceil((x)-0.5):floor((x)+0.5))
>> mex resize.cc
>> % success...
그런데 이상한 점은 math.h에 ceil 함수 등은 있는데 round함수는 없다는 것이 이상함.
어쨌던 성공적으로 컴파일이 되었음. 성공하면 resize.mexw64라는 파일이 생김.
위의 yprime(1,1:4)는 실행하면
>> yprime(1,1:4)
ans =
2.0000 8.9685 4.0000 -1.0947
과 같은 결과가 나옴
features.cc도 mex로 컴파일하고 featpyramid.m파일과 테스트 이미지 파일을 d:\temp_mat\에 복사하여 사용.
아래에 주어진 코드는 DPM에서 사용하는 HOG특징에 대한 것이다. 주어진 영상(여기서는 480x640 pixels)에 대해 다수의 Octave를 구축하여 특징을 얻는다.
관심 물체(사람, 자전거, 자동차, ...)는 카메라와 물체 사이의 거리에 따라 영상 내에서 크기가 달라질 수 있다. 따라서, 모델 크기와 비교하여 달라질 수 있는 다양한 scale에 대해 물체 탐색(일반적으로 sliding window search을 사용)을 수행해야 한다.
다양한 스케일에 대해 물체를 탐색하기 위해 image pyramid를 사용할 수 있다. 먼저, 다양한 영상 크기를 만들고, 각각의 영상에 대해 HOG 특징 값을 추출하여 사용한다.
먼저 테스트할 영상을 입력한다.
>> im=imread('000034.jpg');
함수를 호출하여 특징을 추출한다. 10개의 octave를 구축한다. HOG 특징을 계산할 cell의 크기는 8 pixels을 사용한다.
DPM에서는 HOG를 coarse level과 fine level로 나누어 사용하는데, coarse level에서는 8x8 pixels patch에 대해 HOG를 추출하여 사용하며, fine level은 4x4 pixels patch에서 HOG를 추출하여 사용한다.
추출 순서는 먼저 coarse level에서 8x8 HOG에 의한 물체의 개략적 윤곽(외곽)을 이용하여 물체가 있을 수 있는 위치를 추출하고, 추출된 후보 위치에서 물체를 구성하는 part를 인식할 때는 fine level의 HOG를 사용한다.
>> [feat, scale] = featpyramid(im, 8, 10); % octave내의 스케일 수 = 10
>> size(feat)
ans =
46 1 % 전체 이미지 피라미드는 46단계로 구성
>> size(feat{1}) % 첫번째 영상 특징은 480x640 pixels 영상 크기에 대해
% 118x158개의 31차원 특징 벡터(4x4 cell HOG)가 얻어졌다.
ans =
118 158 31
>> size(scale)
ans =
46 1
아래는 함수의 코드이다.
HOG의 octave구축에 대한 자세한 내용은 code 내의 설명을 참고한다.
HOG의 octave구축에 대한 자세한 내용은 code 내의 설명을 참고한다.
function [feat, scale] = featpyramid(im, sbin, interval)
% [feat, scale] = featpyramid(im, sbin, interval);
% Compute feature pyramid.
%
% sbin is the size of a HOG cell - it should be even.
% interval is the number of scales in an octave of the pyramid.
% feat{i} is the i-th level of the feature pyramid.
% scale{i} is the scaling factor used for the i-th level.
% feat{i+interval} is computed at exactly half the resolution of feat{i}.
% first octave halucinates higher resolution data.
sc = 2 ^(1/interval); % sc=1.0718
imsize = [size(im, 1) size(im, 2)]; % 480x640
max_scale = 1 + floor(log(min(imsize)/(5*sbin))/log(sc)); % 36
feat = cell(max_scale + interval, 1); % 46
scale = zeros(max_scale + interval, 1); % 46
% our resize function wants floating point values
im = double(im);
for i = 1:interval % 1~10
% i=1일 때, scaled=480x640x3(color)
% ~i=10이면, scaled=257x343x3까지 작아짐
scaled = resize(im, 1/sc^(i-1));
% "first" 2x interval
feat{i} = features(scaled, sbin/2); % 118x158x31(i=1),fine level hog
scale(i) = 2/sc^(i-1); % 2
% "second" 2x interval
feat{i+interval} = features(scaled, sbin); %58x78x31(i=1),coarese level
scale(i+interval) = 1/sc^(i-1);
% remaining interals
for j = i+interval:interval:max_scale % j=11,21,31(i=1)
scaled = resize(scaled, 0.5); %240x320x3(i=1,j=11)
feat{j+interval} = features(scaled, sbin); %28x38,31(i=1,j=11)
scale(j+interval) = 0.5 * scale(j); % 0.5
end
% i=1일 때의 iteration에 대해
% feat: 1, 11, (21, 31, 41)이 계산됨(단, 괄호는 j루프에서 계산)
% i=2이면, feat: 2, 12, (22, 32, 42)가 계산...
% i=3, feat: 3, 13, (23, 33, 43), ...
% i=6, feat: 6, 16, (26, 36, 46)
% i=7, feat: 7, 17, (27, 37)
% i=9, feat: 9, 19, (29, 39)
% i=10, feat: 10, 20, (30, 40)
% feat{1~10}까지는 4x4 cell크기의 hog 특징 저장
% 정리하면,
% feat: 1~10까지는 480x640에서 257x343까지 작아지는 10개의 영상에 대해
% 4x4cell hog를 적용하여 특징을 추출한 것
% feat: 11~20까지는 480x640 -> 257x343로 점차 작아지는 영상(10단계)에 대해
% 8x8cell hog를 적용하여 특징 추출
% feat: 21, 31, 41, 480x640을 계속 절반씩 줄이면서(320x240->160x120->80x60)
% 8x8cell을 적용하여 특징을 추출한 것
% feat: 22, 32, 42, 448x597을 계속 절반씩 줄이면서(224x298->...)
% 8x8cell을 적용하여 특징을 추출한 것
% feat: 23, 33, 43, 418x557을 계속 절반씩 줄이면서(209x278->...)
% 8x8cell을 적용하여 특징을 추출한 것
% ... feat: ...
%
% feat을 grouping하면(이것을 octave라고 함)
% 1(480x640,4x4cell),11(480x640,8x8cell),21(240x320,8x8cell),31((120x160,
% 8x8cell),41((60x80,8x8cell)
% 2(448x597,4x4cell),12(448x597,8x8cell),22(224x298,8x8cell),
% 32(112x149,8x8cell),42((56x74,8x8cell)
% ...
% octave가 10개가 생김
end
References
[1] Compiling matlab mex file in Windows 64bit and Matlab 2010a 64bit with VS10.0(VS2010).
관리자 권한으로 매트랩 실행. 압축을 풀기위함. 이후 매트랩 실행시에는 관리자 권한으로 실행할 필요 없음.
>>unzip('d:\temp_mat\S2010MEXSupport.zip', matlabroot); %Matlab 2010a에서 Visual Studio 10.0(VS2010) 컴파일러를 연동시키기 위한 패치파일
>>mex -setup % Visual Studio 10.0 컴파일러를 선택한다.
>>yprime(1,1:4) %실행되지 않는다.
>>mex c:\mex\yprime.c %현재 폴더에 yprime.mexw64 파일이 생성된다.
>>yprime(1, 1:4) %실행됨
참고사항: Visual Studio 2008 SP1은 64bit 컴파일러를 기본적으로 설치하지 않기 때문에 64비트 매트랩 환경에서는 컴파일이 안될수도 있다.
http://www.mathworks.co.kr/support/solutions/en/data/1-6IJJ3L/?solution=1-6IJJ3L
[2] resize.cc 컴파일 방법:
DPM의 소스 코드에 있는 resize.cc 파일에 대해 직접 컴파일 해 보니 몇 함수가 정의되지 않았다는 메시지가 나왔음. 따라서 아래와 같이 추가:
#define bzero(s,n) memset ((s), 0, (n))
#define round(x) (x<0?ceil((x)-0.5):floor((x)+0.5))
>> mex resize.cc
>> % success...
그런데 이상한 점은 math.h에 ceil 함수 등은 있는데 round함수는 없다는 것이 이상함.
어쨌던 성공적으로 컴파일이 되었음. 성공하면 resize.mexw64라는 파일이 생김.
위의 yprime(1,1:4)는 실행하면
>> yprime(1,1:4)
ans =
2.0000 8.9685 4.0000 -1.0947
과 같은 결과가 나옴
features.cc도 mex로 컴파일하고 featpyramid.m파일과 테스트 이미지 파일을 d:\temp_mat\에 복사하여 사용.
2014년 6월 23일 월요일
DPM: Deformable Part Model
자세한 이론적 내용은 [1]을 참고한다. 사용한 프로그램은 Felzenszwalb의 홈페이지에서 다운 받았다. 기본적으로 Matlab을 사용하고 있으며 속도가 필요한 부분은 c로 구현이 되었으며 c 코드를 컴파일해서 mex파일을 생성하고 matlab에서 호출하여 사용하고 있다. version 3.1을 다운받아 사용하였다. 홈페이지[2]를 참조한다.
물체 검출을 실행하는 matlab 파일은 detect.m인데 너무 복잡하다. 별 필요없는 부분을 제거 후 간단해 진 파일이 detect1.m이다 [3].먼저 학습된 모델을 load한다.
>> load car_final.mat
테스트할 영상 파일을 읽는다.
>> im = imread('000034.jpg'); %car image
검출을 실행한다.
>> boxes = detect1(im, model, 0);
결과를 화면에 출력한다.
>> showboxes(im, boxes);
검출된 모든 결과가 overlap으로 출력되어 진짜 솔루션을 찾기가 어렵다.
따라서 non-maximum supp을 수행한 후 다시 출력한다.
>> top = nms(boxes, 0.5);
>> showboxes(im, top);
detect1.m 파일은 실행하는 동안 여러 c언어로 만들어진 함수들을 호출한다. resize.cc, features.cc, fconv.cc, dt.cc 등인데 원 파일은 windows7하의 vs2010에서 컴파일이 되지 않아 주로 header부분을 수정하였다.
DPM의 원래 논문[2]에 있는 테스트 영상에 실행해 보니, 논문에 실린 동일한 결과가 출력 되었다. 직접 찍은 영상을 테스트 해 보기로 한다.
일전에 출근하다가 도로에서 찍은 영상이 있어 테스트를 해 보았다. 아래는 원래 크기의 영상이다. 크기를 좀 줄였는데도 크다.
>> size(im)
ans =
1224 1632 3
>>boxes=detect1(im,model,0);
>>top=nms(boxes,0.5);
>>showboxes(im,top);
뒷 모습이 보이는 큰 차 뿐 만 아니라 반대 차선에서 다가오는 작게 앞면이 보이는 차량 까지도 감지 되었다. 사실 작게 보이지만 이미지 자체가 큰 영상이므로 실제는 작지 않다.
앞 부분에 있는 차는 크기가 매우 커 감지 되었으나, 뒷 부분은 크기가 작아서 감지 되지 않는다.
>> load person_final.mat % 사람을 검출하는 학습 모델을 로드
>> im=imread('people1.jpg'); % 테스트할 영상 입력
>> size(im) % 입력된 영상의 크기 출력
ans =
586 888 3
크기는 앞의 큰 도로 영상보다 더 작다.
>> boxes=detect1(im,model,0); % 사람 검출 실행
>> top=nms(boxes,0.5); % non maximum suppression (다중 응답을 제거)
전체적으로는 잘 검출이 되었으나 양 옆에서 약간 오차가 있는 것 같다.
좀 더 복잡한 영상이다.
>> im=imread('people2.jpg');
>> size(im)
ans =
>> boxes=detect1(im,model,0);
>> showboxes(im,boxes);
검출 윈도가 너무 많이 오버랩이 되어서 결과 확인이 어렵다. 이번에는 nms를 수행해 보았다.
오버랩은 많이 제거 되었으나 오 검출 결과들이 몇 보인다. 아주 멀리 있는 사람 말고 윤곽이 보이는 사람들은 검출이 되었다. Red box가 물체의 root window이고, root box 내부에 있는 Blue box가 part window이다. 차나 사람이나 part는 6개가 설정되었다.
원 논문의 저자 홈페이지에서 코드를 다운받아 설치하여 보면 이미 학습되어 있는 많은 물체 카테고리가 있다.
원 논문의 저자 홈페이지에서 코드를 다운받아 설치하여 보면 이미 학습되어 있는 많은 물체 카테고리가 있다.
load 명령을 통해 모델을 Matlab에 로딩 시키고 car와 human의 경우처럼 테스트 영상에 대해 물체를 감지하면 된다.
새로운 물체를 감지할 필요가 있다면 learning부의 코드를 실행 시켜 위와 같은 물체category.mat 파일을 생성해 주어야 한다.
References
[0] 설정방법
설치 컴퓨터를 바꾸거나 matlab version이 바뀌거나 재설치 시 함수가 실행이 되지 않는 문제가 있다. DPM 코드는 연산량이 많은 부분은 c함수를 통해 계산하기 때문에 c함수를 현재의 설치 환경 하에서 재 컴파일을 해 주어야 한다.
(1) >> mex -setup: 먼저 현재 환경에 맞는 c컴파일러를 선정해 준다. 주어진 명령을 실행하면 사용 가능한 컴파일러가 나타나는데 이 중에서 하나를 선정해 주어야 한다.
(2) 컴파일해주어야 하는 파일은 모두 5개이다. yprime.c, dt.cc, fconv.cc, features.cc, resize.cc이다.
>> mex yprime.c
>> mex dt.cc
> ...
(3) 컴파일된 mex파일이 생성되었다면 detect1.m이 실행될 수 있다.
[1]P. Felzenszwalb, R. Girshick, D. McAllester, D. Ramanan, Object Detection with Discriminatively Trained Part Based Models, IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 32, No. 9, Sep. 2010
[2] http://www.cs.berkeley.edu/~rbg/latent/index.html
[3] d:\temp_mat
[4] Detect1.m:
function [boxes] = detect(input, model, thresh, bbox, ...
overlap, label, fid, id, maxsize)
% boxes = detect(input, model, thresh, bbox, overlap, label, fid, id, maxsize)
% Detect objects in input using a model and a score threshold.
% Higher threshold leads to fewer detections.
%
% The function returns a matrix with one row per detected object. The
% last column of each row gives the score of the detection. The
% column before last specifies the component used for the detection.
% The first 4 columns specify the bounding box for the root filter and
% subsequent columns specify the bounding boxes of each part.
%
% If bbox is not empty, we pick best detection with significant overlap.
% If label and fid are included, we write feature vectors to a data file.
if nargin > 3 && ~isempty(bbox)
latent = true;
else
latent = false;
end
if nargin > 6 && fid ~= 0
write = true;
else
write = false;
end
if nargin < 9
maxsize = inf;
end
% we assume color images
input = color(input); % 아래에서 test하는 영상 크기는 480x640
% prepare model for convolutions
rootfilters = [];
%{
model =
sbin: 8
rootfilters: {[1x1 struct] [1x1 struct]}
offsets: {[1x1 struct] [1x1 struct]}
blocksizes: [1 775 1 744 1085 4 1085 4 620 4 620 4 992 4 496 4 992 4 496 4]
regmult: [0 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
learnmult: [20 1 20 1 1 0.1000 1 0.1000 1 0.1000 1 0.1000 1 0.1000 1 0.1000 1 0.1000 1 0.1000]
lowerbounds: {1x20 cell}
components: {[1x1 struct] [1x1 struct]}
interval: 10
numcomponents: 2
numblocks: 20
partfilters: {1x12 cell}
defs: {1x12 cell}
maxsize: [6 10]
minsize: [5 8]
thresh: -1.3918
%}
%size(model.rootfilters) = 2: 필터가 2개
%size(model.rootfilters{1}.w) = 5 10 31: win patch가 5x10개이고, 각 patch는
%size(model.rootfilters{2}.w) = 6 8 31: 31개의 값을 가지는 vector
for i = 1:length(model.rootfilters)
rootfilters{i} = model.rootfilters{i}.w;
end
partfilters = [];
% size(model.partfilters)=12
% size(model.partfilters{1}.w) = 7 5 31: patch가 7x5개이고 각 patch는 31개의
% size(model.partfilters{2}.w) = 7 5 31: 값을 가지는 vector. 이런 filter가 12개
for i = 1:length(model.partfilters)
partfilters{i} = model.partfilters{i}.w;
end
% cache some data
for c = 1:model.numcomponents % model.numcomponents=2
ridx{c} = model.components{c}.rootindex; % 1, 2
oidx{c} = model.components{c}.offsetindex; % 1, 2
root{c} = model.rootfilters{ridx{c}}.w; % root=[5x10x31]
rsize{c} = [size(root{c},1) size(root{c},2)]; % rsize{1}= 5 10
numparts{c} = length(model.components{c}.parts); % 6
%{
model.components{1}.parts{1}
ans =
partindex: 1
defindex: 1
model.components{1}.parts{2}
ans =
partindex: 2
defindex: 2
...
model.components{2}.parts{1}
ans =
partindex: 7
defindex: 7
...
%}
for j = 1:numparts{c} % 6(c=1)
pidx{c,j} = model.components{c}.parts{j}.partindex;
didx{c,j} = model.components{c}.parts{j}.defindex;
part{c,j} = model.partfilters{pidx{c,j}}.w; % part{1,1}=[7x5x31]
psize{c,j} = [size(part{c,j},1) size(part{c,j},2)]; %psize{1,1}=7 5
% reverse map from partfilter index to (component, part#)
rpidx{pidx{c,j}} = [c j];
end
end
% we pad the feature maps to detect partially visible objects
padx = ceil(model.maxsize(2)/2+1); % model.maxsize= 6 10
pady = ceil(model.maxsize(1)/2+1); % padx=6, pady=4
% the feature pyramid
interval = model.interval; % 10
[feat, scales] = featpyramid(input, model.sbin, interval);
% detect at each scale
best = -inf;
ex = [];
boxes = [];
% level: 1~10: 4x4 Hog가 적용된 pyramid 이미지
for level = interval+1:length(feat) % length(feat)=46 -> level: 11~46
scale = model.sbin/scales(level); % scale=8/1
% size(feat{level}, 1) = 58, size(feat{level}, 2) = 78
if size(feat{level}, 1)+2*pady < model.maxsize(1) || ... % 66<6
size(feat{level}, 2)+2*padx < model.maxsize(2) || ... % 90<10
(write && ftell(fid) >= maxsize)
continue;
end
% convolve feature maps with filters
% size(feat{11})=58 78 31
% size(featr) = 66 90 31: 원이미지(480x640)에 8x8Hog가 적용된 feature img.
% size(featr(:,:,1))=66 90: 즉, patch의 수가 58x78개
featr = padarray(feat{level}, [pady padx 0], 0);
% rootfilters = [5x10x31 double] [6x8x31 double]
% level=11이면 original size(480x640)이미지의 feature patch에 root filter
% 를 conv하여 search 한 것
% ****** root match 계산이 중요
rootmatch = fconv(featr, rootfilters, 1, length(rootfilters));
% rootmatch=[62x81 double] [61x83 double]
if length(partfilters) > 0 %12
% size(featp)=134 182 31, size(feat{1})=118 158 31
featp = padarray(feat{level-interval}, [2*pady 2*padx 0], 0);
% level-interval: level=11이고, interval=10이므로 feat{1}이고 원 이미지
% 에 대한 4x4 Hog 특징을 추출한 것
%{
partfilters=[7x5x31 double] [7x5x31 double] [5x7x31 double] [5x7x31 double]
[5x8x31 double] [5x8x31 double] [8x4x31 double] [8x4x31 double]
[4x8x31 double] [4x8x31 double] [4x8x31 double] [4x8x31 double]
%}
% ****** part match 계산이 중요
partmatch = fconv(featp, partfilters, 1, length(partfilters));
%{
[128x178 double] [128x178 double] [130x176 double] [130x176 double]
[130x175 double] [130x175 double] [127x179 double] [127x179 double]
[131x175 double] [131x175 double] [131x175 double] [131x175 double]
%}
end
for c = 1:model.numcomponents %2
% root score + offset
%{
model.offsets{1} = w: -6.7609, blocklabel: 1
model.offsets{2} = w: -3.4770, blocklabel: 3
ridx = 1, 2, size(rootmatch{1})=62 81
%}
score = rootmatch{ridx{c}} + model.offsets{oidx{c}}.w; % 62x81
% add in parts
for j = 1:numparts{c} % numparts=6, 6
%{
model.defs{1} = anchor: [1 4], w: [0.0227 0.0144 0.0202 0.0024]
blocklabel: 6
model.defs{2} = anchor: [16 4], w: [0.0227 -0.0144 0.0202 0.0024]
model.defs{3} = anchor: [4 1], w: [0.0155 -0.0239 0.0560 -0.0014]
blocklabel: 8
...
model.defs{12} = anchor: [5 5], w: [0.0314 -0.0056 0.0521 -0.0033]
blocklabel: 20
%}
def = model.defs{didx{c,j}}.w; % size(def)=1 4, didx{1,1}=1
anchor = model.defs{didx{c,j}}.anchor; % size(anchor)=1 2
% 1 2 는 rootblock내의 위치가 아닌지?
% the anchor position is shifted to account for misalignment
% between features at different resolutions
ax{c,j} = anchor(1) + 1; % ax=[2]
ay{c,j} = anchor(2) + 1; % ay=[5]
%{
pidx =
[1] [2] [3] [ 4] [ 5] [ 6]
[7] [8] [9] [10] [11] [12]
%}
match = partmatch{pidx{c,j}}; % size(pidx)= 2 6, size(match)=128x178
% size(M)=128x178, Ix=[128 178 int32], Iy=[128 178 int32]
% size(score)=62x81
% ay{c,j}:2:ay{c,j}+...=5:2:127, size(5:2:127)=62
% ax{c,j}:2:ax{c,j}+...=2:2:162, size(2:2:162)=81
[M, Ix{c,j}, Iy{c,j}] = dt(-match, def(1), def(2), def(3), def(4));
score = score - M(ay{c,j}:2:ay{c,j}+2*(size(score,1)-1), ...
ax{c,j}:2:ax{c,j}+2*(size(score,2)-1));
% score = 62x81(score: root)-62x81(M: part)
end
if ~latent
% get all good matches
I = find(score > thresh);
level
I
[Y, X] = ind2sub(size(score), I);
tmp = zeros(length(I), 4*(1+numparts{c})+2);
for i = 1:length(I)
x = X(i);
y = Y(i);
[x1, y1, x2, y2] = rootbox(x, y, scale, padx, pady, rsize{c});
b = [x1 y1 x2 y2];
for j = 1:numparts{c}
[probex, probey, px, py, px1, py1, px2, py2] = ...
partbox(x, y, ax{c,j}, ay{c,j}, scale, padx, pady, ...
psize{c,j}, Ix{c,j}, Iy{c,j});
b = [b px1 py1 px2 py2];
end
tmp(i,:) = [b c score(I(i))];
end
boxes = [boxes; tmp];
end % end of ~latent
end % end of c
end % end of level
피드 구독하기:
덧글 (Atom)