DNN학습할 때, 학습 샘플 수가 작을 경우가 많다. 이 때, 모델은 데이터에 과적합된다. 과적합을 피하기 위해 data augmentation이나, dropout등을 적용하면 학습 자체가 잘 되지 않는 일이 발생한다.
이럴 때 해볼 수 있는 옵션 중에 L2 regularization이 있다.
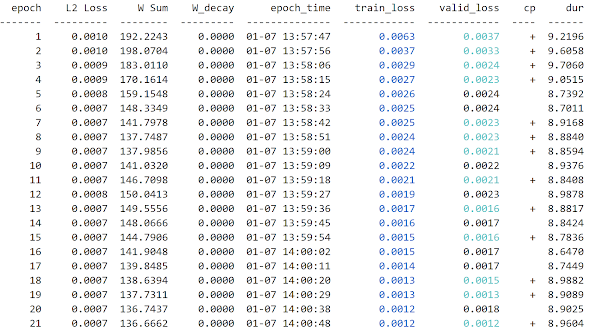
skorch기반으로 다변량 시계열 데이터에 대해 regression학습을 해보면 가중치의 제곱합(Weights Sum)값이 아래와 같다.
valid_loss는 계속 줄고 있지만, 가중치합이 급격히 증가하고 있다. 즉, 모델이 과적합 되고 있다.
이번에는 Loss항에 L2 regularization항을 포함시키고, 다시 학습을 시키면 다음과 같다.
W Sum항을 살펴보면 값이 줄고 있고, 범위 내에서 관리되고 있다. 즉, L2 Loss항과 MSE Loss항이 합쳐져서 train_loss값이 된다.
이 때 L2 Loss의 가중치인 Ramda값의 크기를 잘 결정해 주어야 한다.
- L2 regularization 적용 시, Weights Sum이 작아짐.
- L2 loss의 크기가 최적화되었을 때의 train_loss나 valid_loss의 절반 이하가 되게 Weight_decay값을 선정
- 즉, L2 Loss가 원래 Loss의 감소에 영향을 주지 않을 정도로 Ramda값을 정해 준다.