작성 중...
$V(t)$와 $\omega(t)$는 control input.
로봇의 시작 점과 목표 점이 주어진다고 할 때,
Path는 $P(u)$에 의해 정의된다. 파라메터인 $u$는 0에서 1까지 변하는 값으로 0은 로봇의 시작 점, 1은 목표 점을 가리킨다.
이 수식은 아주 많은 파라메터들로 구성되는데 이 값들을 바꾸면 다양한 형태의 path가 생성된다 [1].
만일 장애물을 회피하여 목표 점까지 이동한다 가정하자. 경로는 시작 위치에서 장애물을 피하고 목표 위치로 부드럽게 수렴하는 경로를 얻는 것이 필요하다.
여러 파라메터 중에서 2개의 파라메터를 고려하면,
$Path=f(\eta_3, \theta_a)$
이고 path는 다양한 파라메터 중에서 두 변수가 중요하게 작용하므로 이들의 함수이다.
현재 로봇이 가진 각도를 기준으로 전방 180도로 정의하면,
$\theta_a$를 0~180에서 10도씩 나누고, 각 $\theta$에 대해 10개의 $\eta$를 정의한다.
그러면 위 그림의 상부와 같은 경로들이 나온다.
즉, 10도씩 나누어 19개의 set가 있고, 각 set 내에는 ($\eta$의 변화에 따라) 10개의 path가 존재한다.
이렇게 정의한 여러 path 중에서 최적인 하나를 선정하는 것이 필요하다.
로봇은 자체 회전이 가능하여 어떤 출발 각도를 가지고도 출발할 수 있다.
이동 경로 길이가 짧으면서 장애물 충돌 없이 목표에 도달하는 것이 필요하다.
예를 들면 출발 각이 목표 각과 비슷하면 경로 길이는 짧아 진다.
경로를 결정하였으면 로봇이 경로를 따라 잘 이동하도록 제어하는 것이 필요하다.
current 위치에서 destination으로 위치와 자세를 바꾸기 위해서 오차를 위 행렬 식처럼 정의한다.
Lyapunov함수를 이용하여 비용함수 $V$를 정의한다. 식을 보면 $x_e, y_e, \theta_e$가 모두 0으로 가면 $V$도 0으로 수렴한다.
References
[1] Lyapunov Theory


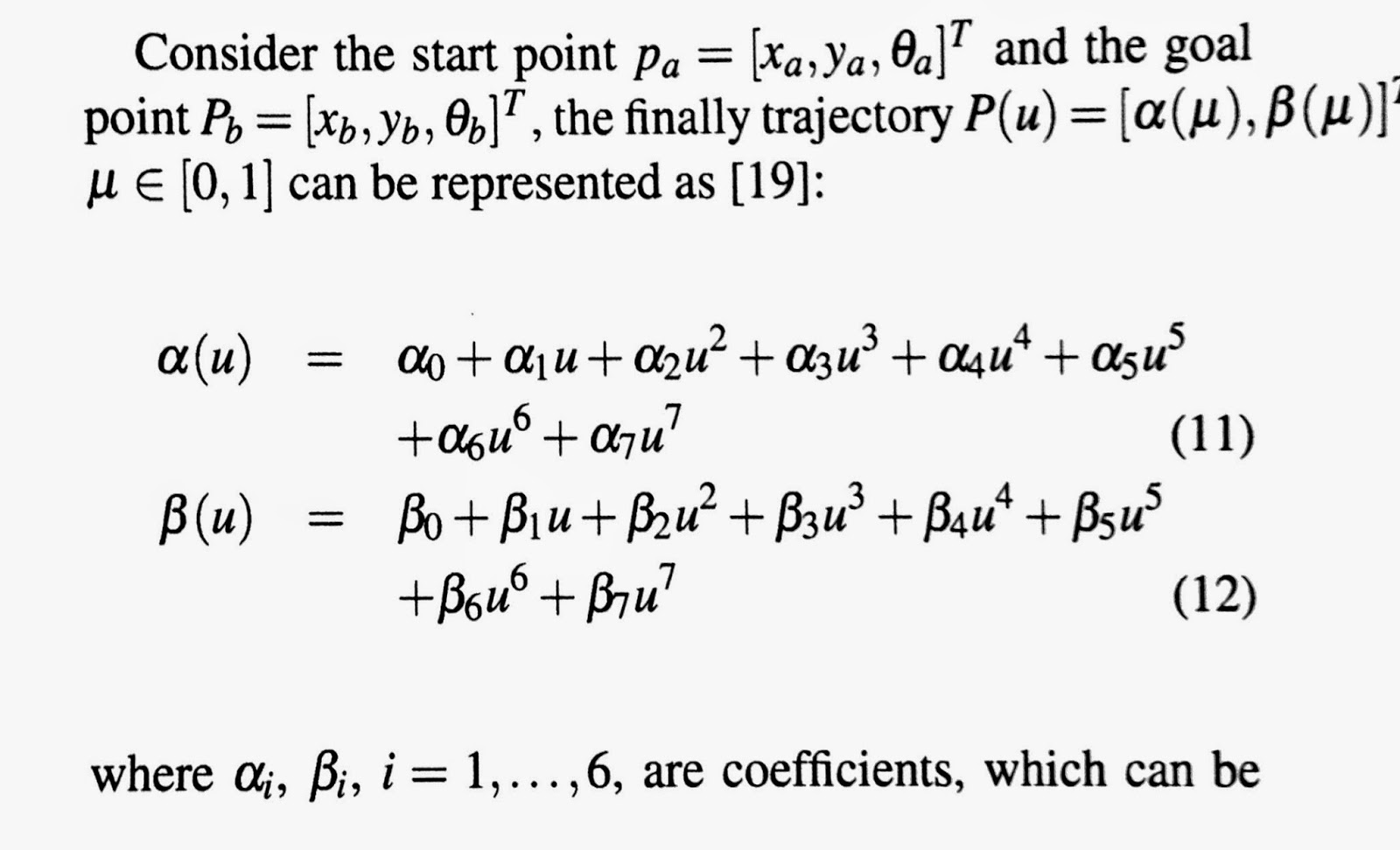



댓글 없음:
댓글 쓰기